
Pavage Ammann A3

Pavage Ammann A4

Pavage Ammann-Beenker

Pavage Ammann-Beenker rhomb triangle

Pavage Ammann chair

Pavage Armchair

Pavage Binary

Pavage Example of canonical 1

Pavage Example of canonical 2

Pavage Chaim's cubic PV

Pavage Chair

Pavage Chair variant

Pavage Coloured golden triangle

Pavage Cubic pinwheel

Pavage Cyclotomic rhombs 7-fold

Pavage Danzer's non-FLC 5

Pavage Danzer's 7-fold

Pavage Danzer's 7-fold variant

Pavage Domino variant 1

Pavage Domino variant 2
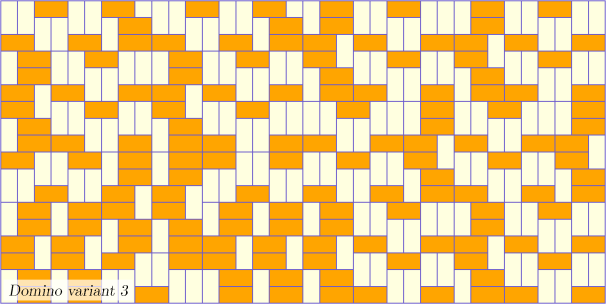
Pavage Domino variant 3

Pavage Equithirds

Pavage Fibonacci times Fibonacci

Pavage Golden pinwheel

Pavage Golden triangle

Pavage Goodman-Strauss 7-fold rhomb

Pavage Half-hex

Pavage Harriss's 4-fold rhomb

Pavage Harriss's 9-fold rhomb
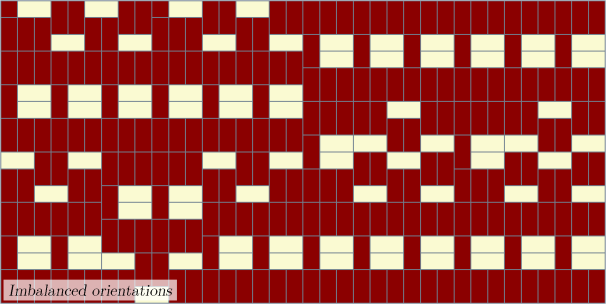
Pavage Imbalanced orientations

Pavage Kenyon's non-FLC

Pavage Kenyon (1, 2, 1) polygon

Pavage Kite-domino

Pavage Limhex

Pavage Lord

Pavage Maloney's 7-fold

Pavage Octagonal 1225

Pavage Penrose kite-dart

Pavage Penrose pentagon boat star

Pavage Penrose rhomb

Pavage Penrose triangle

Pavage Pentomino

Pavage Pinwheel variant 1

Pavage Pinwheel variant 2

Pavage Pinwheel variant 3

Pavage Pinwheel variant 4

Pavage Pinwheel variant 5

Pavage Pinwheel 1-2

Pavage Pinwheel 2-1

Pavage Pinwheel 3-1
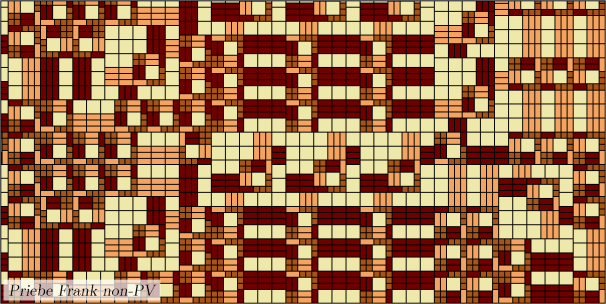
Pavage Priebe Frank non-PV

Pavage Psychedelic Penrose variant 1

Pavage Pythagoras 3-1

Pavage Pythagoras 3-2

Pavage Pythagoras 5-2

Pavage Pythia 3-1

Pavage Quartic pinwheel

Pavage Rhomb square oktagon

Pavage Robinson triangle

Pavage Rorschach

Pavage Semi-detached house

Pavage Semi-detached house squared

Pavage Sierpinski's square

Pavage Sierpinski's triangle

Pavage Shield

Pavage Socolar

Pavage Sphinx

Pavage Sphinx 9

Pavage Sqrt6 triangles

Pavage Square chair

Pavage Square triangle

Pavage Squeeze

Pavage Squiral

Pavage Tangram

Pavage Tetris

Pavage Tipi 3-1

Pavage Triangle duo variant 1

Pavage Triangle duo variant 2

Pavage Triangle duo variant 3

Pavage Trihex

Pavage Tritriangle

Pavage Tuebingen triangle

Pavage Uberpinwheel

Pavage Viper

Pavage Waltonchair

Pavage Watanabe Ito Soma 8-fold

Pavage Watanabe Ito Soma 12-fold variant 1

Pavage Watanabe Ito Soma 12-fold variant 2

Pavage Wheel tiling
Le fichier Cristallo.mac contient un grand nombre de macros permettant de dessiner de nombreux pavages apériodiques. Dans cette page, nous appellerons pavage apériodique un pavage du plan qui n’est pas périodique. Néanmoins, la signification du terme « apériodique » peut varier d’un ouvrage à l’autre. Les pavages réalisés sont ici tous des pavages dits « par substitution » (ou « substitution tiling » en anglais). Cette terminologie désigne la manière dont sont construits ces pavages. Chacun d’entre eux est composé de un ou plusieurs types de tuiles. Pour chacun de ces types de tuiles, on définit une règle de substitution. Celle-ci permet de décomposer un type de tuiles en un ensemble de plusieurs tuiles de base du pavage.
Les noms attribués aux pavages sont pour la plupart ceux définis sur le site d’Edmund Harriss et D. Frettlöh, The Tiling Encyclopedia, qui a servi de base pour l’élaboration de toutes les macros du fichier.